Binary Search Algorithm

Binary Search

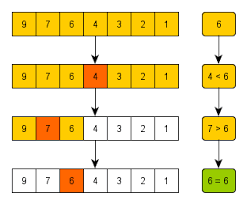Figure [1] Binary Seach Algorithm applied to a descending order list

Let's say we have an ascending-order sorted list of numbers as given below:

number_list = [6, 12, 24, 39, 42, 43, 45, 89]

Say we were tasked with finding whether a particular element was in the list or not, the simplest way that would occur to us is to use a 'for' loop. 

target = 39

for num in number_list:

  if num == target:

    print(f"{num} is in number_list.")

This works but say, we have a huge list of about a million or even a billion values, what would be the worst-case time complexity of such an operation?

It could be that the target is the last item in the list, which results in the time complexity being O(n).

So, let's think about a better way of solving this problem.

Now, we know that the list is ascending-order sorted which means if we check a random number in the list and the number is bigger than our target, we can be sure that our target if it is in, will be to the left of that number. Same thing if the number is smaller than the target, we can then look for the target to the right of the number.

Let's take this one step further. What would be the best place to start with? Probably the middle, cause that way, we can eliminate half the list if number != target. Let's code this out.

# Let's initialize low & high variables to indicate our search range

low = 0

high = len(list) - 1 # We're subtracting 1 since counting starts from 0 for a list

# Let's use a while loop to check all the elements of the list

while low <= high:

  mid = low + (high-low) //2 # Floor division for quotient

  if number_list[mid] == target:

    print(f'Target in list')

  elif number_list[mid] < target:

    low = mid + 1

      elif number_list[mid] > target:

        high = mid - 1

Now, this program has a much better time complexity than our initial one. Analyzing the complexity of the algorithm looks as follows:

Initial length - N

Iteration 1 - N/2

Iteration 2 - N/4 i.e. N/2^2

Iteration 3 - N/8 i.e. N/2^3

...

Iteration k - N/2^k

Since the final length of the array is 1, we can find the

N/2^k = 1

Rearranging the terms, we get

N = 2^k

Taking the logarithm

k = log N

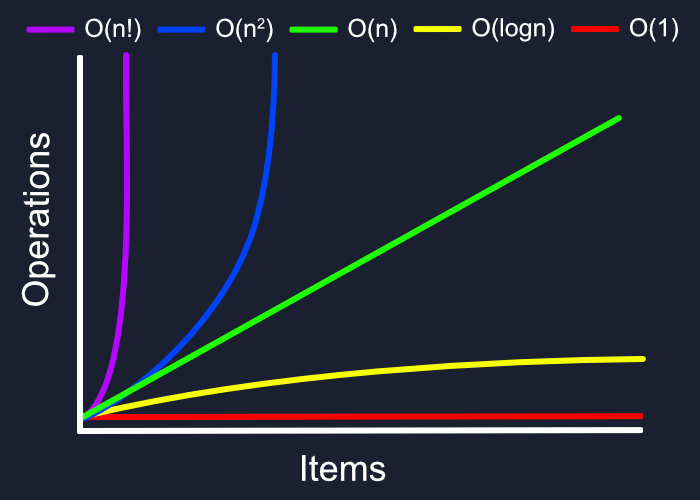
If we graph out, the time complexities of our two solutions, it would look like the following:

The second solution that we came up with is a 'Binary search' algorithm solution. On graphing and comparing to our first 'Linear solution', we see that as the list size grows, the time complexity of log(n) is much more favorable! Big O notation is a mathematical notation that describes the limiting behavior of a function when the argument tends towards a particular value or infinity.

Here's a Leetcode Binary search problem, if you're looking to implement this yourself.

Thank you for reading!

References:

[1] Grokking Algorithm by Aditya (link)

[2] Jovian AI DSA course (link)